存图

所谓图（graph），是图论中基本的数学对象，包括一些顶点，和连接顶点的边，这里的边只是表示顶点的连接情况，用直线或曲线表示均可。图可以分为有向图和无向图，有向图中的边是有方向的，而无向图的边是双向连通的。

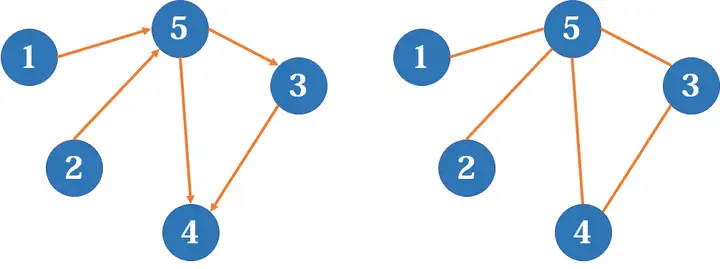
有向图和无向图

算法竞赛中有一些称为图论题的题目，涉及到对图的处理，为了解决它们，我们至少先得把图存储起来，这个过程我们称为存图。

邻接矩阵

谈到存图，最朴素的想法当然是用一个二维数组mat[]存储两个边的连接情况。假如从顶点u到顶点v有一条边，则令mat[u][v] = 1。这种建图方法称为邻接矩阵。例如上面的那张有向图的邻接矩阵是：

1234512345[0000100001000100000000110]

相应地，上面那张无向图的邻接矩阵是：

1234512345[0000100001000110010111110]

这是没有边权的情况，对于有边权（可以理解为边的长度）的图，其实只要把对应的1换成边权即可。

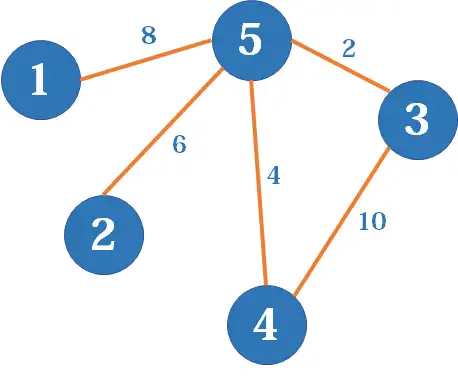
有边权的图

代码也很好写：

//这是双向有边权图的写法，其他类型的图写法类似
inline void add(int u, int v, int w)
{
    mat[u][v] = w;
    mat[v][u] = w;
}

邻接矩阵的优点显而易见：简单好写，查询速度快。但缺点也很明显：空间复杂度太高了。 n 个点对应大小 n2 的数组，如果点的数量达到10000，这种方法就完全不可行了。

事实上，我们可以看到，上面那两个矩阵中有大量的元素是0，有大量空间被浪费了。这虽然使得我们可以迅速判断两个点之间是否没有边，但我们为此付出的代价太大了，我们其实更关注那些确实存在的边。我们希望，可以跳过这些0，直达有边的地方，就像下面这样：

1234512345[−−−→1−−−→1−−→1−−−−−−−→11−]

邻接表

上面那张表可以认为是邻接表的雏形。我们把邻接矩阵的行从数组替换为链表。当然上面那张表并不准确，因为用链表替换数组后，下标也就不复存在了。所以我们需要用一个结构体来同时储存边的终点（相当于邻接矩阵的第二个下标）和权值：

//如果没有边权可以不使用结构体，只存储终点即可
struct Edge
{
    int to, w;
};

那么文中的第一张图的邻接表（无边权）应该长这个样子：

1:2:3:4:5:5543→4

上面那张有边权的图的邻接表则长这个样子：

1:2:3:4:5:5(8)5(6)4(10)→5(2)3(10)→5(4)3(2)→4(10)→2(6)→1(8)

换句话说，邻接表存储每个顶点能够到达哪些顶点。注意这里链表的顺序是无关紧要的，取决于存图的顺序。

接下来按理说我们该实现链表了，但在算法竞赛上手写链表这种动态数据结构，又费时又容易写错，所以我们一般采取以下两种方法代替链表：

std::vector

STL里的vector容器，作为动态数组，既拥有链表节省内存的优点，但又可以以类似数组的方式访问，而且写法也很简便。

std::vector<Edge> edges[MAXN];
inline void add(int from, int to, int w)
{
    Edge e = {to, w};
    edges[from].push_back(e);  //向vector的最后添加一条边
}

对于无向图，调用两次add()即可：

//这对本文所有数据结构都适用
inline void add2(int u, int v, int w)
{
    add(u, v, w);
    add(v, u, w);
}

遍历图时用通常遍历数组的方法即可，注意vector的size()方法可以返回其包含元素的个数。

// 遍历2号点能到达的所有点
for (int i = 0; i < edges[2].size(); ++i)
    printf("%d ", edges[2][i].to); 

也可以用range-based for写成：

for (auto &&e: edges[2])
    printf("%d ", e.to); 

链式前向星

另一种思路是用数组模拟链表，这样的存图方法有一个听上去很高端的名字：链式前向星。因为STL常数大，我个人更喜欢这种方法。不过它写起来稍微复杂一点。

struct Edge
{
    int to, w, next;
}edges[MAXM];
int head[MAXN], cnt; // cnt为当前边的编号
inline void add(int from, int to, int w)
{
    edges[++cnt].w = w;    //新增一条编号为cnt+1的边，边权为w
    edges[cnt].to = to;    //该边的终点为to
    edges[cnt].next = head[from];  //把下一条边，设置为当前起点的第一条边
    head[from] = cnt;  //该边成为当前起点新的第一条边
}

我们为每条边额外储存一个属性next，并赋予每条边一个编号。head数组则用于储存每个起点对应的第一条边。

为了理解链式前向星存图的过程，我们用一张无权值有向图来举个例子：

一开始，没有点，也没有边，所有数组为空且cnt=0。现在我们add(1,2)：

这时我们拥有了一条编号为1的边（注意1是编号不是权值），1号边的起点是1号顶点，现在1号顶点没有连接任何边，于是head[1]自然为1。然后1号边通往2号顶点，所以edges[1].to=2。head[1]原本为0，于是edges[1].next=0，这其实就是遍历结束的标志。

然后我们add(1,3)。

这时新增一条编号为2的边，通往3号顶点。这条新的边“鸠占鹊巢”成为新的head[1]，原来的head[1]成为它的next。然后我们add(2,4)。

到这里已经很明显了，如果你有关注图片最右边的那张表，会发现那就是邻接表。它跟std::vector的一个区别在于，它会把新元素添加到最前面而不是最后面。（也许这就是叫“前”向星的原因？）

遍历链式前向星的时候稍微复杂一点，类似于链表的遍历，例如：

//打印2号顶点能到达的所有点
for (int e = head[2]; e != 0; e = edges[e].next)
    printf("%d ", edges[e].to);

本文介绍了三种存图的方法，除了邻接矩阵对内存的消耗太大外，另两种方法在大部分题目都可以互换使用，主要取决于个人喜好。当然，存图只是图论题基础中的基础，具体的图论算法还需要后续慢慢学习。